Table of Contents
List of Figures
- 1.1. Kidekin TRNG (without epoxy fill option)
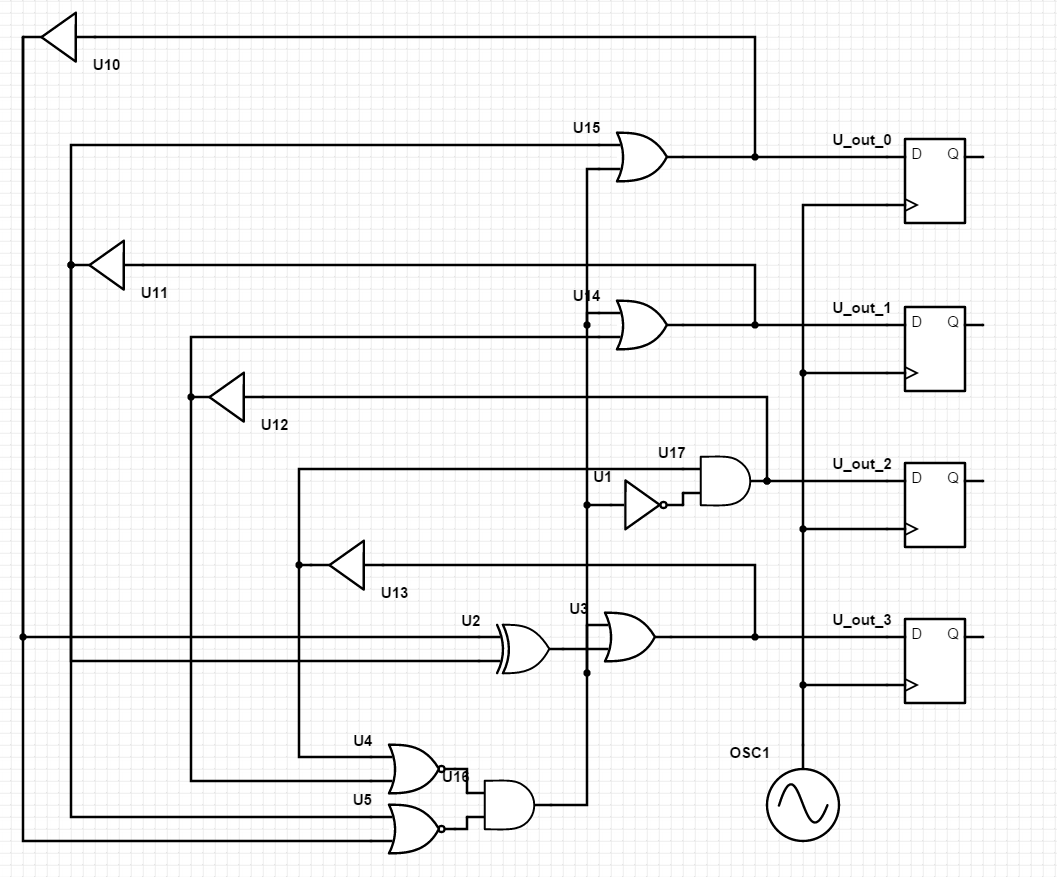
- 2.1. Conceptual schematic of a 4 bit register-less LFSR
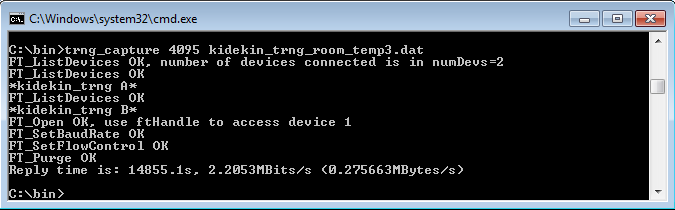
- 3.1. trng_capture output after creating a file of almost 4GB
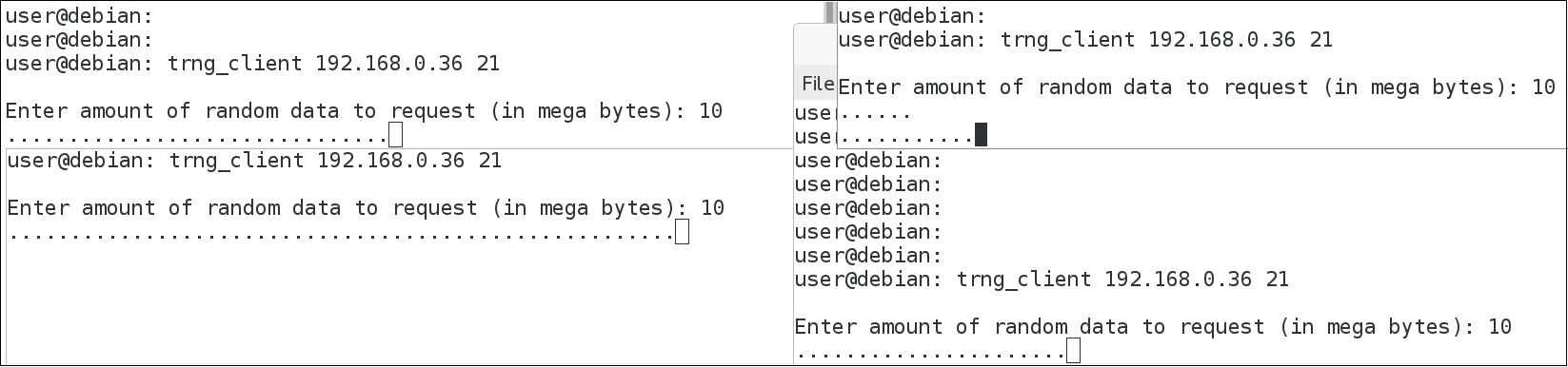
- 3.2. Several trng_client instances accessing the same trng_server in parallel
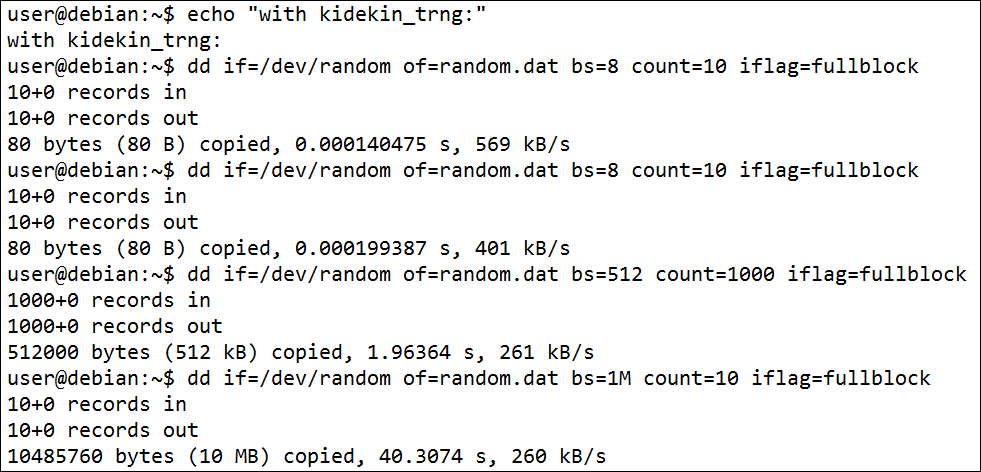
- 3.3. /dev/kidekin_trng typical performances: about 40 seconds to generate 10 mega bytes.
- 3.4. /dev/random typical performances
- 3.5. /dev/random with Kidekin TRNG typical performances
Kidekin TRNG is a true random number generator in the popular "USB key" form factor which can be used in multiple ways on various platforms. The documentation is therefore broken down in several documents, each focusing on a particular task or use case. This document describe the hardware and present the content of the software package.
Kidekin TRNG contains a purely digital entropy source rather than analogue one. It delivers full entropy bits at a rate higher than 2Mbits/s (275Kbytes/s). As the entropy source is purely digital, it is much more stable than analogue sources with respect to operating conditions as well as process variations. The randomness comes from an array of small free running oscillators, like in most papers on the subject.
Unlike typical implementation, the oscillators are "register-less LFSRs" with remapping of the null state. This allows to harness entropy from two phenomenon:
- The chaotic behavior of such "LFSRs"
- The lack of synchronization between them
The complex feedback structure also avoid the "self alignment" tendency often found with arrays of ring oscillators. Kidekin TRNG implement 8 such LFSRs running in parallel, output is sampled at 96MHz. The sampled data is then compressed by a standard CRC-8 circuit to produce output bytes.
The raw random bits have a very good entropy out of the box, estimation tools typically report higher than 7.9 bits of entropy per byte.
Entropy estimation over a 956MB file of raw random bits:
- min-entropy: 7.996690052203161
- shannon-entropy: 7.999999658975694
- NIST’s frequency test entropy: 7.975869236184793 (as described in SP800-90B 9.3.7.3)
About entropy report by the tool "ent"
ent reports the shannon entropy, and it makes rounding errors on big data files. It reported 8.0 bits/bytes on the same 956MB file.
It allows to make the full entropy claim and follows NIST’s SP800-90B recommendations: it is a CBC-MAC using AES-128 encryption. It is done in hardware and cannot be switch off. As a result the device does not have any configuration, making it user friendly and hard to misuse. The access to the raw entropy bits is useful only during the design phase anyway, to know how many blocks the CBC-MAC should process to achieve full entropy. With 7.9 bits of entropy per byte, 3 blocks are enough, actually this would be enough even with 6.7 bits of entropy per byte, so this provides a large safety margin. This is an option because some people may prefer to mix the raw bits with other entropy sources and then perform their favourite cryptographic post processing.
The software package contains ready made software to use Kidekin TRNG. The following information can be useful if you whish to build your own software or linux’s udev rules.
lsusb command to find the device:
user@debian:$sudo lsusb Bus 001 Device 001: ID 1d6b:0001 Linux Foundation 1.1 root hub Bus 001 Device 002: ID 80ee:0021 VirtualBox USB Tablet Bus 001 Device 006: ID 0403:6010 Future Technology Devices International, Ltd FT2232C Dual USB-UART/FIFO IC
Kidekin TRNG is based on the USB chip "FT2232C Dual USB-UART/FIFO IC". In this example there is only one such device so we know right away that it is the TRNG. If they are several, the fields inside the device descriptor structure contain unambiguous identifiers.
lsusb output showing device descriptor structure (extract):
user@debian:$sudo lsusb -s 001:006 -v
Bus 001 Device 006: ID 0403:6010 Future Technology Devices International, Ltd FT2232C Dual USB-UART/FIFO IC
Device Descriptor:
bLength 18
bDescriptorType 1
bcdUSB 1.10
bDeviceClass 0 (Defined at Interface level)
bDeviceSubClass 0
bDeviceProtocol 0
bMaxPacketSize0 64
idVendor 0x0403 Future Technology Devices International, Ltd
idProduct 0x6010 FT2232C Dual USB-UART/FIFO IC
bcdDevice 7.00
iManufacturer 1 kidekin
iProduct 2 kidekin_trng
iSerial 3 20150523AES0000
bNumConfigurations 1
Configuration Descriptor:
bLength 9
bDescriptorType 2
wTotalLength 55
bNumInterfaces 2
bConfigurationValue 1
iConfiguration 0
bmAttributes 0x80
(Bus Powered)
MaxPower 500mA
Interface Descriptor:
bLength 9
bDescriptorType 4
bInterfaceNumber 0
bAlternateSetting 0
bNumEndpoints 2
bInterfaceClass 255 Vendor Specific Class
bInterfaceSubClass 255 Vendor Specific Subclass
bInterfaceProtocol 255 Vendor Specific Protocol
iInterface 2 kidekin_trng
The number idVendor is always equal to 0x0403 and the idProduct always equal to 0x6010 however this is not specific to Kidekin TRNG.
The fields iManufacturer and iProduct are specific to Kidekin TRNG and can be use to filter all connected TRNGs
The number iSerial (line 17), is unique for each device. It consist of three fields.
Serial number fields
- Fabrication date (YYYYMMDD format)
Configuration
- RAW: the device output raw random numbers
- AES: the device has the CBC-MAC AES128 post processor
- Daily serial number: an hexadecimal number unique for each device programmed on the same day.
About USB interfaces
The device contains two USB interface, random numbers are available only on the "B" interface. Sending commands or reading the "A" interface can "brick" the device. Sending commands to the "B" interface can also "brick" the device. In summary, only read operation on the "B" interface is supported.
The default casing is a white vinyl sticker simply wrapped around the PCB. It protects against light coffee spills only. The optional filling is made in hard epoxy, it is injected within the sticker, protecting the electronics from pretty much anything, including the worse coffee spills :-). If the white cover is peeled-off, it is then tamper-evident, unless one goes through the pain of replicating the filling after damaging it… This option is expensive because it involves a lot of manual work with nasty substances.
The dimensions vary slightly depending if you have epoxy filling or not:
- Without epoxy filling: 26x102x7 (rounded corners)
- With epoxy filling: 29x98x10 (square corners)
As both casing are handmade, the dimensions may also vary from one sample to another by few millimeters.
The quality of the output has been checked using several tools. For all tests, the data has been gathered using trng_capture.exe. Unless otherwise stated, the tests are run on a file of 954MB (that’s a bit more than 1 billion bits).
RNG test tools:
- ent: an open source program available in many Linux distributions (http://www.fourmilab.ch/random/)
- dat_analysis::entropy: custom entropy estimation tool
- AIS31: AIS31 reference program from BSI. Test run on 4 MB files.
- STS: NIST’s STS 2.1.2 (http://csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html). Data is processed as 1000 streams of 1 million bits.
- Dieharder: Robert G. Brown’s dieharder, version 3.31.1 (http://www.phy.duke.edu/~rgb/General/dieharder.php). Test run on 4095MB files, command "dieharder -a -g 201 -f file_name".
The folder "doc/rpt" of the software package contain those reports and additional ones like cold temperature, hot temperature.
ent report:
Entropy = 8.000000 bits per byte. Optimum compression would reduce the size of this 1000341504 byte file by 0 percent. Chi square distribution for 1000341504 samples is 259.21, and randomly would exceed this value 41.49 percent of the times. Arithmetic mean value of data bytes is 127.4978 (127.5 = random). Monte Carlo value for Pi is 3.141736948 (error 0.00 percent). Serial correlation coefficient is -0.000005 (totally uncorrelated = 0.0).
dat_analysis::entropy report:
min_entropy 7.996690052203161 shannon_entropy 7.999999658975694 frequency_test_entropy 7.975869236184793
Links to AIS31 reports:
STS report:
------------------------------------------------------------------------------
RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES
------------------------------------------------------------------------------
generator is <data/kidekin_trng_room_temp.dat>
------------------------------------------------------------------------------
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
------------------------------------------------------------------------------
105 114 86 102 108 108 97 90 105 85 0.429923 993/1000 Frequency
113 107 102 99 100 88 111 86 97 97 0.635037 992/1000 BlockFrequency
108 94 94 90 94 112 102 103 95 108 0.818343 992/1000 CumulativeSums
105 110 102 106 98 84 94 83 106 112 0.410055 991/1000 CumulativeSums
97 107 103 98 105 111 89 111 83 96 0.570792 991/1000 Runs
97 99 92 100 92 104 128 99 95 94 0.350485 985/1000 LongestRun
106 80 112 112 107 101 76 118 96 92 0.040901 987/1000 Rank
100 112 105 94 99 78 90 85 113 124 0.040108 991/1000 FFT
107 92 108 90 89 119 103 99 94 99 0.528111 992/1000 NonOverlappingTemplate
101 105 95 91 92 96 108 101 100 111 0.912724 994/1000 NonOverlappingTemplate
86 99 92 99 107 113 115 92 106 91 0.450297 990/1000 NonOverlappingTemplate
89 114 102 89 88 117 101 115 108 77 0.049664 992/1000 NonOverlappingTemplate
97 106 90 99 98 115 103 100 100 92 0.877083 989/1000 NonOverlappingTemplate
90 75 103 77 103 100 125 105 121 101 0.004908 991/1000 NonOverlappingTemplate
118 93 87 111 109 101 99 92 89 101 0.408275 987/1000 NonOverlappingTemplate
113 98 99 89 109 123 91 81 84 113 0.038565 992/1000 NonOverlappingTemplate
84 104 107 98 103 92 103 92 93 124 0.278461 995/1000 NonOverlappingTemplate
103 104 83 108 97 105 90 104 100 106 0.775337 985/1000 NonOverlappingTemplate
99 95 107 89 93 109 93 113 97 105 0.761719 991/1000 NonOverlappingTemplate
89 97 107 91 109 113 101 96 100 97 0.801865 993/1000 NonOverlappingTemplate
100 91 95 93 127 103 99 94 101 97 0.401199 993/1000 NonOverlappingTemplate
89 97 100 100 85 98 110 102 114 105 0.653773 992/1000 NonOverlappingTemplate
77 106 102 107 95 100 97 114 95 107 0.417219 992/1000 NonOverlappingTemplate
87 83 107 109 89 95 116 107 117 90 0.112708 992/1000 NonOverlappingTemplate
105 96 104 88 92 99 105 99 105 107 0.932333 991/1000 NonOverlappingTemplate
116 91 83 122 93 92 77 103 94 129 0.001770 992/1000 NonOverlappingTemplate
117 99 95 109 89 109 111 71 96 104 0.068571 988/1000 NonOverlappingTemplate
105 101 103 105 99 102 88 118 85 94 0.540204 994/1000 NonOverlappingTemplate
92 105 93 91 102 107 94 112 103 101 0.866097 982/1000 NonOverlappingTemplate
91 100 118 81 92 95 106 108 100 109 0.322135 988/1000 NonOverlappingTemplate
104 95 89 105 101 118 112 92 80 104 0.251837 989/1000 NonOverlappingTemplate
85 114 105 98 89 106 97 116 94 96 0.415422 990/1000 NonOverlappingTemplate
92 114 85 94 98 122 97 94 109 95 0.236810 994/1000 NonOverlappingTemplate
98 101 99 93 105 107 97 110 86 104 0.875539 989/1000 NonOverlappingTemplate
95 101 101 97 105 101 91 108 95 106 0.975644 997/1000 NonOverlappingTemplate
96 104 93 106 94 97 102 102 107 99 0.987896 992/1000 NonOverlappingTemplate
103 86 100 113 89 105 117 101 98 88 0.385543 987/1000 NonOverlappingTemplate
101 89 97 110 102 99 102 106 98 96 0.965860 994/1000 NonOverlappingTemplate
111 86 113 106 89 92 99 109 95 100 0.520102 989/1000 NonOverlappingTemplate
95 90 97 95 99 118 106 88 109 103 0.581082 990/1000 NonOverlappingTemplate
102 112 105 100 110 85 94 94 103 95 0.735908 992/1000 NonOverlappingTemplate
105 95 81 102 100 99 124 97 109 88 0.199045 986/1000 NonOverlappingTemplate
91 99 100 100 91 108 111 96 103 101 0.927677 994/1000 NonOverlappingTemplate
96 121 106 96 102 90 95 84 125 85 0.042255 987/1000 NonOverlappingTemplate
97 90 107 105 101 109 96 106 96 93 0.922855 995/1000 NonOverlappingTemplate
93 100 105 78 94 103 101 84 121 121 0.042531 995/1000 NonOverlappingTemplate
109 96 98 90 97 108 105 103 91 103 0.912724 986/1000 NonOverlappingTemplate
93 100 90 90 106 122 101 103 99 96 0.538182 994/1000 NonOverlappingTemplate
111 105 100 105 93 72 104 96 88 126 0.029205 988/1000 NonOverlappingTemplate
99 119 95 100 103 86 93 102 105 98 0.664168 991/1000 NonOverlappingTemplate
104 110 95 117 101 77 111 99 94 92 0.223648 991/1000 NonOverlappingTemplate
91 120 85 103 107 97 111 82 97 107 0.173770 992/1000 NonOverlappingTemplate
97 104 88 111 101 105 94 110 88 102 0.739918 992/1000 NonOverlappingTemplate
95 97 83 112 111 89 88 92 115 118 0.100709 988/1000 NonOverlappingTemplate
101 95 100 92 88 105 99 89 101 130 0.170922 995/1000 NonOverlappingTemplate
102 114 85 92 104 103 91 111 103 95 0.585209 994/1000 NonOverlappingTemplate
111 106 90 100 97 99 92 93 97 115 0.725829 987/1000 NonOverlappingTemplate
101 97 100 93 102 111 91 123 93 89 0.380407 985/1000 NonOverlappingTemplate
95 112 94 109 92 99 94 123 94 88 0.278461 994/1000 NonOverlappingTemplate
106 99 88 111 102 93 110 85 109 97 0.564639 985/1000 NonOverlappingTemplate
96 103 105 116 109 87 94 98 91 101 0.660012 991/1000 NonOverlappingTemplate
93 108 107 90 104 112 101 112 96 77 0.267573 993/1000 NonOverlappingTemplate
98 118 93 104 92 102 96 98 108 91 0.713641 989/1000 NonOverlappingTemplate
120 98 98 106 86 97 103 98 102 92 0.605916 986/1000 NonOverlappingTemplate
80 97 88 124 79 109 109 118 86 110 0.005128 991/1000 NonOverlappingTemplate
97 86 111 102 112 78 91 102 112 109 0.177628 984/1000 NonOverlappingTemplate
104 87 98 92 107 113 105 107 92 95 0.705466 992/1000 NonOverlappingTemplate
96 109 117 88 107 87 111 97 85 103 0.267573 989/1000 NonOverlappingTemplate
115 98 109 111 110 99 101 92 84 81 0.205531 989/1000 NonOverlappingTemplate
94 93 111 94 104 102 86 114 112 90 0.439122 991/1000 NonOverlappingTemplate
105 105 101 94 107 103 106 92 95 92 0.949278 986/1000 NonOverlappingTemplate
99 108 94 105 111 109 102 102 83 87 0.540204 989/1000 NonOverlappingTemplate
98 100 92 88 109 89 130 113 85 96 0.045088 992/1000 NonOverlappingTemplate
112 98 94 110 112 99 87 86 106 96 0.488534 990/1000 NonOverlappingTemplate
112 85 79 86 92 97 116 109 106 118 0.038062 993/1000 NonOverlappingTemplate
110 106 96 104 89 89 98 112 91 105 0.674543 988/1000 NonOverlappingTemplate
108 96 102 98 108 87 109 106 92 94 0.800005 993/1000 NonOverlappingTemplate
88 101 97 104 108 106 95 97 114 90 0.739918 990/1000 NonOverlappingTemplate
87 91 97 102 108 103 105 109 101 97 0.873987 992/1000 NonOverlappingTemplate
111 102 111 105 107 83 91 91 112 87 0.286836 987/1000 NonOverlappingTemplate
114 110 86 103 97 87 98 103 100 102 0.641284 989/1000 NonOverlappingTemplate
98 88 104 114 98 94 91 102 103 108 0.781106 987/1000 NonOverlappingTemplate
107 94 106 90 88 120 103 98 93 101 0.506194 992/1000 NonOverlappingTemplate
101 104 100 111 93 99 79 111 106 96 0.532132 988/1000 NonOverlappingTemplate
84 99 84 88 117 105 100 117 106 100 0.164425 989/1000 NonOverlappingTemplate
89 105 85 100 98 108 96 111 94 114 0.526105 991/1000 NonOverlappingTemplate
112 90 98 99 104 106 104 101 90 96 0.887645 991/1000 NonOverlappingTemplate
101 104 105 94 94 114 89 94 128 77 0.037566 990/1000 NonOverlappingTemplate
95 95 95 108 83 104 98 92 121 109 0.323668 994/1000 NonOverlappingTemplate
105 113 101 95 100 118 104 97 85 82 0.263572 994/1000 NonOverlappingTemplate
109 103 100 104 103 99 82 107 84 109 0.508172 985/1000 NonOverlappingTemplate
111 96 107 93 84 106 105 88 111 99 0.516113 989/1000 NonOverlappingTemplate
116 93 95 105 98 111 92 109 87 94 0.504219 987/1000 NonOverlappingTemplate
95 109 95 90 113 95 110 91 98 104 0.713641 989/1000 NonOverlappingTemplate
93 114 91 101 107 101 96 92 103 102 0.859637 996/1000 NonOverlappingTemplate
123 97 125 92 102 75 86 93 102 105 0.011383 986/1000 NonOverlappingTemplate
98 103 102 103 90 102 95 104 107 96 0.984415 993/1000 NonOverlappingTemplate
96 100 109 107 93 96 92 109 94 104 0.906069 988/1000 NonOverlappingTemplate
109 105 102 107 95 91 117 97 93 84 0.467322 988/1000 NonOverlappingTemplate
125 105 94 91 89 114 96 80 96 110 0.063615 985/1000 NonOverlappingTemplate
101 107 103 108 98 98 89 102 93 101 0.961869 990/1000 NonOverlappingTemplate
128 98 112 87 98 87 106 102 89 93 0.095426 989/1000 NonOverlappingTemplate
110 88 87 110 101 120 98 93 98 95 0.353733 994/1000 NonOverlappingTemplate
112 104 100 104 88 91 98 101 100 102 0.904708 989/1000 NonOverlappingTemplate
103 112 84 110 88 92 105 111 98 97 0.459717 989/1000 NonOverlappingTemplate
98 97 97 102 97 95 106 113 96 99 0.971006 988/1000 NonOverlappingTemplate
110 106 94 84 89 107 99 104 105 102 0.695200 986/1000 NonOverlappingTemplate
89 115 97 88 113 95 106 106 90 101 0.469232 994/1000 NonOverlappingTemplate
106 97 96 107 112 99 91 104 86 102 0.786830 990/1000 NonOverlappingTemplate
89 92 110 113 115 107 97 94 97 86 0.368587 991/1000 NonOverlappingTemplate
93 94 103 103 106 116 102 92 101 90 0.775337 990/1000 NonOverlappingTemplate
86 97 111 83 97 86 118 100 110 112 0.126658 993/1000 NonOverlappingTemplate
87 98 112 123 107 114 107 79 90 83 0.019857 991/1000 NonOverlappingTemplate
95 105 111 86 125 105 94 87 96 96 0.184549 992/1000 NonOverlappingTemplate
125 106 88 99 94 120 89 102 86 91 0.058243 986/1000 NonOverlappingTemplate
105 101 101 107 89 104 89 102 110 92 0.832561 989/1000 NonOverlappingTemplate
108 93 89 107 91 113 93 102 103 101 0.743915 985/1000 NonOverlappingTemplate
112 94 94 98 91 116 88 99 94 114 0.406499 987/1000 NonOverlappingTemplate
104 102 84 108 107 92 106 106 106 85 0.548314 991/1000 NonOverlappingTemplate
91 106 104 99 103 110 90 94 104 99 0.914025 990/1000 NonOverlappingTemplate
108 101 117 99 101 83 101 101 99 90 0.587274 990/1000 NonOverlappingTemplate
98 103 88 97 91 99 112 94 115 103 0.676615 991/1000 NonOverlappingTemplate
108 80 108 89 117 100 101 92 98 107 0.307077 991/1000 NonOverlappingTemplate
123 111 89 95 109 106 95 85 87 100 0.148653 990/1000 NonOverlappingTemplate
110 104 93 110 98 99 78 112 101 95 0.415422 979/1000 * NonOverlappingTemplate
88 108 80 108 115 105 100 91 103 102 0.337688 995/1000 NonOverlappingTemplate
94 93 107 109 90 109 96 103 105 94 0.849708 990/1000 NonOverlappingTemplate
102 100 102 97 90 108 94 104 106 97 0.972382 991/1000 NonOverlappingTemplate
94 101 99 87 108 112 115 86 102 96 0.478839 992/1000 NonOverlappingTemplate
88 101 94 107 100 102 108 100 100 100 0.965083 991/1000 NonOverlappingTemplate
86 94 123 104 110 87 95 104 101 96 0.272977 993/1000 NonOverlappingTemplate
87 99 98 96 103 113 91 99 104 110 0.773405 991/1000 NonOverlappingTemplate
95 92 100 87 113 92 102 111 118 90 0.319084 995/1000 NonOverlappingTemplate
103 90 107 104 96 112 100 92 96 100 0.901959 991/1000 NonOverlappingTemplate
107 87 110 102 95 102 110 106 95 86 0.628790 993/1000 NonOverlappingTemplate
110 112 85 112 103 97 92 89 96 104 0.486588 990/1000 NonOverlappingTemplate
109 96 95 97 90 99 106 86 104 118 0.530120 994/1000 NonOverlappingTemplate
103 95 116 95 87 83 113 94 99 115 0.211064 989/1000 NonOverlappingTemplate
115 78 97 107 103 92 88 105 106 109 0.258307 989/1000 NonOverlappingTemplate
94 94 92 94 94 111 98 111 120 92 0.420827 991/1000 NonOverlappingTemplate
102 117 96 104 106 93 109 104 96 73 0.185555 995/1000 NonOverlappingTemplate
98 107 98 93 96 103 113 107 101 84 0.733899 991/1000 NonOverlappingTemplate
89 106 86 99 95 115 104 110 98 98 0.607993 995/1000 NonOverlappingTemplate
95 107 88 94 98 111 118 105 91 93 0.476911 994/1000 NonOverlappingTemplate
99 110 84 101 101 104 105 94 105 97 0.859637 990/1000 NonOverlappingTemplate
87 92 86 104 98 104 102 118 98 111 0.420827 989/1000 NonOverlappingTemplate
108 106 111 92 84 96 107 94 105 97 0.662091 992/1000 NonOverlappingTemplate
100 117 101 106 83 91 100 99 98 105 0.610070 994/1000 NonOverlappingTemplate
103 87 106 97 103 84 96 101 105 118 0.480771 990/1000 NonOverlappingTemplate
95 90 103 102 115 93 95 111 101 95 0.755819 989/1000 NonOverlappingTemplate
84 102 122 105 104 82 97 106 103 95 0.220159 994/1000 NonOverlappingTemplate
105 105 86 103 101 100 110 89 100 101 0.853049 989/1000 NonOverlappingTemplate
112 99 78 105 74 116 115 108 80 113 0.003657 989/1000 NonOverlappingTemplate
96 100 89 109 100 90 96 99 95 126 0.322135 991/1000 NonOverlappingTemplate
95 100 114 97 111 100 81 102 97 103 0.601766 986/1000 NonOverlappingTemplate
97 89 104 113 98 95 92 102 102 108 0.851383 987/1000 NonOverlappingTemplate
106 113 115 100 101 93 95 93 90 94 0.647530 992/1000 OverlappingTemplate
108 101 99 84 90 102 110 113 83 110 0.286836 987/1000 Universal
97 91 121 108 97 98 101 95 93 99 0.653773 991/1000 ApproximateEntropy
55 60 75 54 63 63 58 65 66 60 0.780132 609/619 RandomExcursions
61 54 69 62 79 48 65 65 63 53 0.237412 607/619 RandomExcursions
50 59 72 63 62 69 61 60 64 59 0.798751 617/619 RandomExcursions
62 70 60 67 55 58 64 59 56 68 0.903699 615/619 RandomExcursions
48 56 50 63 63 61 76 71 72 59 0.178012 612/619 RandomExcursions
64 55 63 64 61 54 54 76 60 68 0.630292 612/619 RandomExcursions
58 55 56 52 64 68 60 66 67 73 0.657592 613/619 RandomExcursions
65 50 57 67 80 54 59 63 64 60 0.341275 614/619 RandomExcursions
64 67 63 58 61 71 62 45 82 46 0.038548 613/619 RandomExcursionsVariant
65 62 68 64 60 68 59 67 45 61 0.647360 612/619 RandomExcursionsVariant
70 56 51 68 83 65 54 58 54 60 0.117173 615/619 RandomExcursionsVariant
66 56 63 56 65 78 61 62 54 58 0.609831 617/619 RandomExcursionsVariant
66 54 68 57 59 63 74 70 49 59 0.443349 617/619 RandomExcursionsVariant
58 75 53 61 71 66 49 76 56 54 0.132590 614/619 RandomExcursionsVariant
57 68 56 75 59 56 65 63 60 60 0.786394 614/619 RandomExcursionsVariant
56 55 75 58 74 51 48 69 74 59 0.079874 611/619 RandomExcursionsVariant
61 53 65 68 53 54 47 69 88 61 0.016832 617/619 RandomExcursionsVariant
59 54 57 69 71 60 57 61 66 65 0.853839 610/619 RandomExcursionsVariant
57 63 54 59 52 59 65 63 73 74 0.529198 610/619 RandomExcursionsVariant
51 53 62 55 61 69 70 64 71 63 0.582671 614/619 RandomExcursionsVariant
53 50 58 63 70 62 73 61 63 66 0.592833 615/619 RandomExcursionsVariant
51 59 66 66 71 68 59 62 60 57 0.804842 615/619 RandomExcursionsVariant
44 69 80 65 59 61 71 56 55 59 0.098397 612/619 RandomExcursionsVariant
50 69 63 66 58 52 73 69 63 56 0.449467 615/619 RandomExcursionsVariant
59 65 57 59 70 69 45 55 77 63 0.208728 613/619 RandomExcursionsVariant
62 58 66 67 54 59 58 61 62 72 0.899148 610/619 RandomExcursionsVariant
92 99 110 98 96 102 100 89 114 100 0.829047 993/1000 Serial
85 102 93 101 90 114 115 92 107 101 0.424453 993/1000 Serial
95 102 77 112 106 108 114 97 89 100 0.257004 993/1000 LinearComplexity
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The minimum pass rate for each statistical test with the exception of the
random excursion (variant) test is approximately = 980 for a
sample size = 1000 binary sequences.
The minimum pass rate for the random excursion (variant) test
is approximately = 605 for a sample size = 619 binary sequences.
For further guidelines construct a probability table using the MAPLE program
provided in the addendum section of the documentation.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Dieharder report:
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name | filename |rands/second|
file_input_raw| kidekin_trng_room_temp3.dat| 1.83e+07 |
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.83863430| PASSED
diehard_operm5| 0| 1000000| 100|0.99859410| WEAK
diehard_rank_32x32| 0| 40000| 100|0.51382007| PASSED
diehard_rank_6x8| 0| 100000| 100|0.10267084| PASSED
diehard_bitstream| 0| 2097152| 100|0.88208024| PASSED
diehard_opso| 0| 2097152| 100|0.91301645| PASSED
diehard_oqso| 0| 2097152| 100|0.02761662| PASSED
diehard_dna| 0| 2097152| 100|0.45052643| PASSED
diehard_count_1s_str| 0| 256000| 100|0.95293866| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.97542713| PASSED
diehard_parking_lot| 0| 12000| 100|0.08478625| PASSED
diehard_2dsphere| 2| 8000| 100|0.55320976| PASSED
diehard_3dsphere| 3| 4000| 100|0.67713221| PASSED
diehard_squeeze| 0| 100000| 100|0.39622256| PASSED
diehard_sums| 0| 100| 100|0.00055826| WEAK
diehard_runs| 0| 100000| 100|0.15831810| PASSED
diehard_runs| 0| 100000| 100|0.72414595| PASSED
diehard_craps| 0| 200000| 100|0.15854166| PASSED
diehard_craps| 0| 200000| 100|0.54455765| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.53455546| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.64239498| PASSED
sts_monobit| 1| 100000| 100|0.92818270| PASSED
sts_runs| 2| 100000| 100|0.06724033| PASSED
sts_serial| 1| 100000| 100|0.87600831| PASSED
sts_serial| 2| 100000| 100|0.56154264| PASSED
sts_serial| 3| 100000| 100|0.64654782| PASSED
sts_serial| 3| 100000| 100|0.49536253| PASSED
sts_serial| 4| 100000| 100|0.96794326| PASSED
sts_serial| 4| 100000| 100|0.21215232| PASSED
sts_serial| 5| 100000| 100|0.62022036| PASSED
sts_serial| 5| 100000| 100|0.67405245| PASSED
sts_serial| 6| 100000| 100|0.59645346| PASSED
sts_serial| 6| 100000| 100|0.11123998| PASSED
sts_serial| 7| 100000| 100|0.70530969| PASSED
sts_serial| 7| 100000| 100|0.98588862| PASSED
sts_serial| 8| 100000| 100|0.76323783| PASSED
sts_serial| 8| 100000| 100|0.63409086| PASSED
sts_serial| 9| 100000| 100|0.82979927| PASSED
sts_serial| 9| 100000| 100|0.26994653| PASSED
sts_serial| 10| 100000| 100|0.77875408| PASSED
sts_serial| 10| 100000| 100|0.83002735| PASSED
sts_serial| 11| 100000| 100|0.96012132| PASSED
sts_serial| 11| 100000| 100|0.94885291| PASSED
sts_serial| 12| 100000| 100|0.96963305| PASSED
sts_serial| 12| 100000| 100|0.86876144| PASSED
sts_serial| 13| 100000| 100|0.60116582| PASSED
sts_serial| 13| 100000| 100|0.90825798| PASSED
sts_serial| 14| 100000| 100|0.96992212| PASSED
sts_serial| 14| 100000| 100|0.08302696| PASSED
sts_serial| 15| 100000| 100|0.25821694| PASSED
sts_serial| 15| 100000| 100|0.08524629| PASSED
sts_serial| 16| 100000| 100|0.92167076| PASSED
sts_serial| 16| 100000| 100|0.64124003| PASSED
rgb_bitdist| 1| 100000| 100|0.99492755| PASSED
rgb_bitdist| 2| 100000| 100|0.37422725| PASSED
rgb_bitdist| 3| 100000| 100|0.25111928| PASSED
rgb_bitdist| 4| 100000| 100|0.99131473| PASSED
rgb_bitdist| 5| 100000| 100|0.50172020| PASSED
rgb_bitdist| 6| 100000| 100|0.08420173| PASSED
rgb_bitdist| 7| 100000| 100|0.02720214| PASSED
rgb_bitdist| 8| 100000| 100|0.98873574| PASSED
rgb_bitdist| 9| 100000| 100|0.78506885| PASSED
rgb_bitdist| 10| 100000| 100|0.69138581| PASSED
rgb_bitdist| 11| 100000| 100|0.24619433| PASSED
rgb_bitdist| 12| 100000| 100|0.76975707| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.58627042| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.39183036| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.66326334| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.11244814| PASSED
rgb_permutations| 2| 100000| 100|0.36235424| PASSED
rgb_permutations| 3| 100000| 100|0.56448535| PASSED
rgb_permutations| 4| 100000| 100|0.45403203| PASSED
rgb_permutations| 5| 100000| 100|0.44613056| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.59273953| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.54615979| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.57226025| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.56568533| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.99379904| PASSED
rgb_lagged_sum| 5| 1000000| 100|0.92276883| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.66744623| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.99801725| WEAK
rgb_lagged_sum| 8| 1000000| 100|0.71690013| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.63687697| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.17728644| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.93282847| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.62586317| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.39088813| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.69165592| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.05122127| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.36057874| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.22182933| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.64380525| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.59682895| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.53549386| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.14822566| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.43138556| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.05137599| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.75091496| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.13600277| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.77984991| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.03258301| PASSED
rgb_lagged_sum| 28| 1000000| 100|0.00168794| WEAK
rgb_lagged_sum| 29| 1000000| 100|0.85706626| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.56700009| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.03074607| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.36619883| PASSED
rgb_kstest_test| 0| 10000| 1000|0.27993323| PASSED
dab_bytedistrib| 0| 51200000| 1|0.09171790| PASSED
dab_dct| 256| 50000| 1|0.33065847| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.28755577| PASSED
dab_filltree| 32| 15000000| 1|0.16933372| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.95758231| PASSED
dab_filltree2| 1| 5000000| 1|0.13145078| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.26835334| PASSED
ent report:
Entropy = 8.000000 bits per byte. Optimum compression would reduce the size of this 1002438656 byte file by 0 percent. Chi square distribution for 1002438656 samples is 265.93, and randomly would exceed this value 30.61 percent of the times. Arithmetic mean value of data bytes is 127.5056 (127.5 = random). Monte Carlo value for Pi is 3.141427002 (error 0.01 percent). Serial correlation coefficient is -0.000003 (totally uncorrelated = 0.0).
dat_analysis::entropy report:
min_entropy 7.996826369401534 shannon_entropy 7.999999606137532 frequency_test_entropy 7.976073562136397
Links to AIS31 reports:
STS report:
------------------------------------------------------------------------------
RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES
------------------------------------------------------------------------------
generator is <data\kidekin_trng_aespp_room_temp.dat>
------------------------------------------------------------------------------
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
------------------------------------------------------------------------------
106 87 90 103 93 100 117 94 101 109 0.564639 994/1000 Frequency
95 101 107 85 95 123 88 98 101 107 0.310049 986/1000 BlockFrequency
95 100 84 99 97 96 99 103 113 114 0.655854 993/1000 CumulativeSums
105 83 96 112 97 93 99 104 99 112 0.643366 995/1000 CumulativeSums
92 97 115 93 96 109 107 90 100 101 0.745908 990/1000 Runs
96 89 105 86 110 105 116 102 85 106 0.347257 993/1000 LongestRun
111 114 96 103 73 82 99 102 118 102 0.044508 985/1000 Rank
103 97 104 94 112 106 106 92 100 86 0.792508 990/1000 FFT
114 86 111 100 107 97 103 97 86 99 0.548314 988/1000 NonOverlappingTemplate
91 128 95 93 94 111 93 99 93 103 0.211064 990/1000 NonOverlappingTemplate
99 93 91 97 121 94 109 103 89 104 0.490483 989/1000 NonOverlappingTemplate
91 82 95 101 83 114 96 113 125 100 0.044797 990/1000 NonOverlappingTemplate
105 109 105 99 102 100 90 79 97 114 0.454053 993/1000 NonOverlappingTemplate
116 99 103 100 92 81 117 111 87 94 0.159910 989/1000 NonOverlappingTemplate
104 110 88 101 105 105 91 91 100 105 0.836048 991/1000 NonOverlappingTemplate
102 81 99 100 104 114 103 100 103 94 0.707513 992/1000 NonOverlappingTemplate
104 110 92 93 111 107 90 108 108 77 0.239266 989/1000 NonOverlappingTemplate
93 95 112 115 115 95 89 106 94 86 0.288249 994/1000 NonOverlappingTemplate
119 121 80 81 87 101 94 93 106 118 0.009603 988/1000 NonOverlappingTemplate
92 98 107 95 94 96 110 99 97 112 0.877083 991/1000 NonOverlappingTemplate
94 96 113 87 116 104 90 94 110 96 0.424453 992/1000 NonOverlappingTemplate
96 102 97 97 89 99 124 97 96 103 0.564639 989/1000 NonOverlappingTemplate
111 110 114 95 90 99 90 103 101 87 0.512137 989/1000 NonOverlappingTemplate
89 90 88 102 100 107 92 118 109 105 0.426272 990/1000 NonOverlappingTemplate
114 86 84 93 96 86 106 133 100 102 0.015707 985/1000 NonOverlappingTemplate
75 110 98 103 103 101 110 95 106 99 0.428095 993/1000 NonOverlappingTemplate
107 100 105 101 98 112 94 94 88 101 0.883171 980/1000 NonOverlappingTemplate
104 110 98 102 106 92 96 98 92 102 0.959347 993/1000 NonOverlappingTemplate
97 93 95 104 101 94 112 103 99 102 0.966626 993/1000 NonOverlappingTemplate
113 115 88 98 85 98 100 99 104 100 0.546283 987/1000 NonOverlappingTemplate
84 105 104 90 99 92 96 120 111 99 0.350485 989/1000 NonOverlappingTemplate
97 98 97 105 118 115 97 85 90 98 0.406499 992/1000 NonOverlappingTemplate
103 104 103 110 100 100 103 84 87 106 0.735908 989/1000 NonOverlappingTemplate
107 113 90 112 94 94 101 102 80 107 0.360287 989/1000 NonOverlappingTemplate
103 96 105 105 93 103 100 95 104 96 0.992952 985/1000 NonOverlappingTemplate
91 120 98 94 96 106 97 108 87 103 0.510153 989/1000 NonOverlappingTemplate
105 89 100 84 105 96 89 113 106 113 0.402962 994/1000 NonOverlappingTemplate
102 122 93 92 90 94 92 109 107 99 0.408275 994/1000 NonOverlappingTemplate
97 105 89 108 94 104 96 106 100 101 0.954015 989/1000 NonOverlappingTemplate
113 107 110 93 86 83 100 107 101 100 0.435430 991/1000 NonOverlappingTemplate
113 94 108 95 109 98 97 98 88 100 0.801865 988/1000 NonOverlappingTemplate
87 98 86 95 119 94 112 110 114 85 0.103753 992/1000 NonOverlappingTemplate
102 92 122 89 106 100 115 101 91 82 0.145326 990/1000 NonOverlappingTemplate
100 109 94 112 95 96 97 94 101 102 0.940080 988/1000 NonOverlappingTemplate
96 108 102 90 97 88 91 112 95 121 0.328297 991/1000 NonOverlappingTemplate
91 85 115 90 114 101 107 84 105 108 0.201189 986/1000 NonOverlappingTemplate
101 107 109 105 94 84 109 105 94 92 0.684890 987/1000 NonOverlappingTemplate
93 107 101 103 97 93 98 103 103 102 0.992670 993/1000 NonOverlappingTemplate
105 95 94 94 127 90 94 88 97 116 0.123755 991/1000 NonOverlappingTemplate
82 93 103 122 101 96 109 112 85 97 0.144504 991/1000 NonOverlappingTemplate
112 91 107 94 112 90 99 101 98 96 0.763677 988/1000 NonOverlappingTemplate
90 112 104 114 90 111 84 101 98 96 0.388990 990/1000 NonOverlappingTemplate
101 112 95 108 110 99 89 86 111 89 0.442831 987/1000 NonOverlappingTemplate
88 92 112 102 110 97 86 103 88 122 0.163513 988/1000 NonOverlappingTemplate
105 102 95 103 98 107 97 99 92 102 0.992381 990/1000 NonOverlappingTemplate
96 98 95 102 115 114 97 93 99 91 0.729870 992/1000 NonOverlappingTemplate
100 98 109 89 101 105 90 100 95 113 0.811080 986/1000 NonOverlappingTemplate
123 96 99 88 86 104 96 101 123 84 0.048093 990/1000 NonOverlappingTemplate
104 103 102 120 97 103 97 104 75 95 0.260930 990/1000 NonOverlappingTemplate
98 103 109 91 87 115 78 107 110 102 0.209948 989/1000 NonOverlappingTemplate
89 100 91 99 110 80 123 116 88 104 0.057510 992/1000 NonOverlappingTemplate
101 97 106 89 106 102 114 97 103 85 0.693142 995/1000 NonOverlappingTemplate
98 99 95 90 111 110 96 106 94 101 0.883171 990/1000 NonOverlappingTemplate
113 84 108 102 85 111 90 100 99 108 0.347257 989/1000 NonOverlappingTemplate
104 97 91 103 99 104 106 97 104 95 0.988291 990/1000 NonOverlappingTemplate
80 103 101 103 98 110 118 86 111 90 0.179584 988/1000 NonOverlappingTemplate
88 104 102 96 91 103 105 101 103 107 0.939005 994/1000 NonOverlappingTemplate
106 92 121 114 90 103 93 106 86 89 0.187581 996/1000 NonOverlappingTemplate
118 101 106 106 89 114 86 89 93 98 0.286836 987/1000 NonOverlappingTemplate
96 83 104 95 104 88 101 96 117 116 0.298282 988/1000 NonOverlappingTemplate
94 87 94 94 103 89 126 103 101 109 0.228367 986/1000 NonOverlappingTemplate
90 89 106 111 100 101 101 92 113 97 0.717714 992/1000 NonOverlappingTemplate
113 124 82 113 102 90 105 92 91 88 0.056069 988/1000 NonOverlappingTemplate
103 94 96 105 81 109 107 104 106 95 0.684890 984/1000 NonOverlappingTemplate
89 90 93 96 96 115 105 113 95 108 0.524101 991/1000 NonOverlappingTemplate
86 86 101 87 94 90 99 114 105 138 0.004908 994/1000 NonOverlappingTemplate
104 87 112 95 99 108 108 108 89 90 0.566688 990/1000 NonOverlappingTemplate
104 114 120 83 90 82 101 91 127 88 0.006661 990/1000 NonOverlappingTemplate
77 90 105 113 109 109 100 100 110 87 0.184549 989/1000 NonOverlappingTemplate
106 98 106 109 104 96 93 101 97 90 0.942198 990/1000 NonOverlappingTemplate
98 93 107 99 88 87 98 114 92 124 0.183547 993/1000 NonOverlappingTemplate
97 90 83 103 106 106 108 103 96 108 0.707513 989/1000 NonOverlappingTemplate
114 86 110 100 109 96 103 97 86 99 0.530120 988/1000 NonOverlappingTemplate
99 114 123 96 82 93 102 90 101 100 0.202268 990/1000 NonOverlappingTemplate
97 99 97 104 87 98 106 106 98 108 0.942198 989/1000 NonOverlappingTemplate
97 108 114 105 104 84 101 101 91 95 0.664168 991/1000 NonOverlappingTemplate
107 106 92 108 89 90 122 83 101 102 0.206629 988/1000 NonOverlappingTemplate
115 107 78 107 96 114 106 88 97 92 0.175691 983/1000 NonOverlappingTemplate
98 110 93 105 113 103 102 75 105 96 0.329850 990/1000 NonOverlappingTemplate
87 103 122 86 101 97 92 114 99 99 0.255705 994/1000 NonOverlappingTemplate
93 107 93 99 85 114 106 93 117 93 0.357000 992/1000 NonOverlappingTemplate
114 91 103 117 99 111 95 93 81 96 0.244236 993/1000 NonOverlappingTemplate
109 108 103 89 90 95 99 100 93 114 0.693142 985/1000 NonOverlappingTemplate
104 99 89 88 93 93 111 103 114 106 0.593478 990/1000 NonOverlappingTemplate
87 113 88 109 105 109 99 114 89 87 0.239266 990/1000 NonOverlappingTemplate
98 90 116 109 81 99 119 78 107 103 0.047785 989/1000 NonOverlappingTemplate
115 99 92 95 104 91 101 97 102 104 0.881662 985/1000 NonOverlappingTemplate
105 96 92 100 77 106 107 108 94 115 0.316052 987/1000 NonOverlappingTemplate
95 126 96 109 94 92 105 103 92 88 0.249284 989/1000 NonOverlappingTemplate
98 81 97 97 96 105 116 116 96 98 0.387264 985/1000 NonOverlappingTemplate
105 100 90 96 108 118 102 82 102 97 0.465415 989/1000 NonOverlappingTemplate
95 106 109 95 99 120 88 97 103 88 0.461612 986/1000 NonOverlappingTemplate
88 83 112 103 93 129 106 80 96 110 0.016261 989/1000 NonOverlappingTemplate
123 90 110 88 101 93 113 82 94 106 0.094285 982/1000 NonOverlappingTemplate
89 104 102 105 98 98 111 105 103 85 0.784927 991/1000 NonOverlappingTemplate
117 107 99 98 95 86 106 90 93 109 0.504219 989/1000 NonOverlappingTemplate
109 95 100 87 94 97 100 92 116 110 0.595549 985/1000 NonOverlappingTemplate
105 91 99 108 92 120 90 100 92 103 0.526105 990/1000 NonOverlappingTemplate
106 114 110 111 93 84 91 105 105 81 0.186566 991/1000 NonOverlappingTemplate
103 90 110 100 110 110 97 82 102 96 0.572847 989/1000 NonOverlappingTemplate
97 105 101 100 108 98 101 118 79 93 0.420827 987/1000 NonOverlappingTemplate
90 95 105 99 94 137 104 88 86 102 0.023866 996/1000 NonOverlappingTemplate
107 124 101 85 110 96 93 91 92 101 0.235589 991/1000 NonOverlappingTemplate
105 111 92 92 81 98 117 92 97 115 0.199045 987/1000 NonOverlappingTemplate
95 87 93 114 86 118 113 94 114 86 0.076658 989/1000 NonOverlappingTemplate
112 89 98 89 87 116 100 95 119 95 0.199045 987/1000 NonOverlappingTemplate
88 98 97 100 94 108 107 102 103 103 0.952152 994/1000 NonOverlappingTemplate
87 96 105 85 107 106 125 87 95 107 0.126658 993/1000 NonOverlappingTemplate
92 100 105 88 80 110 108 119 95 103 0.217857 989/1000 NonOverlappingTemplate
97 111 102 114 96 88 99 103 89 101 0.717714 995/1000 NonOverlappingTemplate
105 100 64 104 98 104 87 128 100 110 0.004146 988/1000 NonOverlappingTemplate
103 97 94 96 101 97 94 119 99 100 0.853049 991/1000 NonOverlappingTemplate
99 101 121 108 105 95 94 80 95 102 0.332970 991/1000 NonOverlappingTemplate
99 104 104 96 98 95 97 102 111 94 0.981417 990/1000 NonOverlappingTemplate
105 110 89 96 97 110 95 107 91 100 0.811080 982/1000 NonOverlappingTemplate
103 109 107 99 95 111 105 96 84 91 0.674543 989/1000 NonOverlappingTemplate
97 106 105 99 96 96 88 94 113 106 0.844641 990/1000 NonOverlappingTemplate
105 96 90 91 104 111 107 101 100 95 0.887645 990/1000 NonOverlappingTemplate
106 112 111 90 73 95 105 98 114 96 0.123755 995/1000 NonOverlappingTemplate
116 111 82 117 102 86 89 99 104 94 0.135720 985/1000 NonOverlappingTemplate
113 90 92 100 98 105 89 106 110 97 0.711601 990/1000 NonOverlappingTemplate
109 99 107 100 101 90 99 99 107 89 0.908760 993/1000 NonOverlappingTemplate
124 90 112 94 86 89 81 115 104 105 0.035174 980/1000 NonOverlappingTemplate
82 114 116 106 96 92 112 87 105 90 0.149495 995/1000 NonOverlappingTemplate
95 96 98 103 95 92 113 102 100 106 0.940080 986/1000 NonOverlappingTemplate
96 84 109 112 80 101 94 111 109 104 0.241741 990/1000 NonOverlappingTemplate
107 97 98 103 102 93 81 112 99 108 0.643366 992/1000 NonOverlappingTemplate
101 90 103 106 88 110 96 103 107 96 0.851383 987/1000 NonOverlappingTemplate
101 112 99 85 106 73 112 100 116 96 0.077607 989/1000 NonOverlappingTemplate
102 89 100 111 98 100 114 81 104 101 0.510153 988/1000 NonOverlappingTemplate
110 94 97 105 105 92 107 106 93 91 0.856359 987/1000 NonOverlappingTemplate
111 119 80 100 107 98 98 95 94 98 0.347257 987/1000 NonOverlappingTemplate
106 119 114 74 99 93 110 88 105 92 0.056785 987/1000 NonOverlappingTemplate
113 105 100 97 97 86 98 109 94 101 0.807412 990/1000 NonOverlappingTemplate
90 98 107 91 96 99 99 112 101 107 0.878618 984/1000 NonOverlappingTemplate
105 96 120 104 91 90 104 90 106 94 0.508172 990/1000 NonOverlappingTemplate
93 99 86 106 103 106 94 116 88 109 0.490483 995/1000 NonOverlappingTemplate
87 97 104 103 98 99 102 110 105 95 0.934599 991/1000 NonOverlappingTemplate
98 95 90 115 103 92 113 93 113 88 0.385543 988/1000 NonOverlappingTemplate
86 111 99 86 118 101 98 92 98 111 0.325206 993/1000 NonOverlappingTemplate
81 89 97 101 108 99 95 102 123 105 0.249284 992/1000 NonOverlappingTemplate
107 91 91 103 96 115 96 94 100 107 0.777265 988/1000 NonOverlappingTemplate
99 105 114 86 91 104 101 106 94 100 0.751866 990/1000 NonOverlappingTemplate
89 91 114 104 98 105 99 112 94 94 0.678686 993/1000 NonOverlappingTemplate
104 98 102 102 102 98 112 109 96 77 0.528111 988/1000 NonOverlappingTemplate
98 88 84 103 106 106 108 103 96 108 0.701366 989/1000 NonOverlappingTemplate
108 116 100 112 87 96 96 102 89 94 0.508172 984/1000 OverlappingTemplate
118 110 97 99 110 92 91 88 101 94 0.474986 984/1000 Universal
90 105 106 106 101 107 74 107 113 91 0.201189 989/1000 ApproximateEntropy
60 72 79 55 56 58 65 56 64 59 0.446255 620/624 RandomExcursions
65 52 70 64 61 59 63 61 64 65 0.953179 617/624 RandomExcursions
52 65 70 65 68 50 67 66 61 60 0.680688 619/624 RandomExcursions
50 55 64 58 71 59 72 74 49 72 0.155443 616/624 RandomExcursions
54 68 62 59 63 66 61 60 50 81 0.330000 618/624 RandomExcursions
59 52 63 50 58 72 70 54 69 77 0.189030 614/624 RandomExcursions
64 67 52 58 69 59 70 71 68 46 0.325007 612/624 RandomExcursions
60 62 79 64 56 70 57 52 61 63 0.489351 616/624 RandomExcursions
54 64 65 67 62 56 65 63 64 64 0.980447 618/624 RandomExcursionsVariant
53 60 76 63 64 52 68 51 62 75 0.243993 620/624 RandomExcursionsVariant
55 68 65 65 64 64 56 65 45 77 0.289209 619/624 RandomExcursionsVariant
52 71 57 57 69 61 61 55 66 75 0.501993 619/624 RandomExcursionsVariant
52 62 60 63 64 73 59 62 53 76 0.501993 617/624 RandomExcursionsVariant
58 50 55 74 60 77 54 68 59 69 0.216971 617/624 RandomExcursionsVariant
54 64 59 63 51 73 56 67 70 67 0.576895 619/624 RandomExcursionsVariant
50 61 55 71 65 54 72 60 61 75 0.347880 619/624 RandomExcursionsVariant
53 44 55 72 67 61 54 82 69 67 0.034801 622/624 RandomExcursionsVariant
67 44 57 58 75 53 71 63 73 63 0.136777 617/624 RandomExcursionsVariant
66 50 63 56 64 69 52 72 72 60 0.443251 615/624 RandomExcursionsVariant
74 56 64 59 61 56 70 61 72 51 0.501993 612/624 RandomExcursionsVariant
72 49 79 62 64 66 56 52 67 57 0.195729 617/624 RandomExcursionsVariant
60 65 68 58 55 64 66 64 59 65 0.980447 617/624 RandomExcursionsVariant
61 50 50 74 63 63 61 64 52 86 0.035174 617/624 RandomExcursionsVariant
57 46 61 65 52 77 55 59 70 82 0.031273 618/624 RandomExcursionsVariant
60 45 62 74 53 57 63 69 71 70 0.218820 618/624 RandomExcursionsVariant
59 56 59 74 50 62 58 65 69 72 0.501993 618/624 RandomExcursionsVariant
95 86 102 111 99 107 104 97 99 100 0.896345 989/1000 Serial
107 98 92 92 112 91 92 122 98 96 0.371941 988/1000 Serial
96 105 89 104 85 108 118 96 105 94 0.467322 988/1000 LinearComplexity
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The minimum pass rate for each statistical test with the exception of the
random excursion (variant) test is approximately = 980 for a
sample size = 1000 binary sequences.
The minimum pass rate for the random excursion (variant) test
is approximately = 610 for a sample size = 624 binary sequences.
For further guidelines construct a probability table using the MAPLE program
provided in the addendum section of the documentation.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Dieharder report:
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name | filename |rands/second|
file_input_raw|kidekin_trng_aespp_room_temp2.dat| 1.54e+07 |
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.06690462| PASSED
diehard_operm5| 0| 1000000| 100|0.96256527| PASSED
diehard_rank_32x32| 0| 40000| 100|0.86968772| PASSED
diehard_rank_6x8| 0| 100000| 100|0.58061967| PASSED
diehard_bitstream| 0| 2097152| 100|0.43973508| PASSED
diehard_opso| 0| 2097152| 100|0.04087902| PASSED
diehard_oqso| 0| 2097152| 100|0.09108243| PASSED
diehard_dna| 0| 2097152| 100|0.26593410| PASSED
diehard_count_1s_str| 0| 256000| 100|0.14926226| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.86543829| PASSED
diehard_parking_lot| 0| 12000| 100|0.30644186| PASSED
diehard_2dsphere| 2| 8000| 100|0.45678363| PASSED
diehard_3dsphere| 3| 4000| 100|0.69106203| PASSED
diehard_squeeze| 0| 100000| 100|0.32883107| PASSED
diehard_sums| 0| 100| 100|0.00551459| PASSED
diehard_runs| 0| 100000| 100|0.23977400| PASSED
diehard_runs| 0| 100000| 100|0.99458350| PASSED
diehard_craps| 0| 200000| 100|0.14557669| PASSED
diehard_craps| 0| 200000| 100|0.96679653| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.81763467| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.14778603| PASSED
sts_monobit| 1| 100000| 100|0.09356876| PASSED
sts_runs| 2| 100000| 100|0.96152550| PASSED
sts_serial| 1| 100000| 100|0.06413064| PASSED
sts_serial| 2| 100000| 100|0.99520218| WEAK
sts_serial| 3| 100000| 100|0.41817663| PASSED
sts_serial| 3| 100000| 100|0.19713108| PASSED
sts_serial| 4| 100000| 100|0.43306108| PASSED
sts_serial| 4| 100000| 100|0.49425335| PASSED
sts_serial| 5| 100000| 100|0.48045877| PASSED
sts_serial| 5| 100000| 100|0.89728331| PASSED
sts_serial| 6| 100000| 100|0.89441164| PASSED
sts_serial| 6| 100000| 100|0.70870484| PASSED
sts_serial| 7| 100000| 100|0.87999775| PASSED
sts_serial| 7| 100000| 100|0.29340040| PASSED
sts_serial| 8| 100000| 100|0.48574863| PASSED
sts_serial| 8| 100000| 100|0.86999729| PASSED
sts_serial| 9| 100000| 100|0.85848036| PASSED
sts_serial| 9| 100000| 100|0.83023230| PASSED
sts_serial| 10| 100000| 100|0.45085625| PASSED
sts_serial| 10| 100000| 100|0.43870266| PASSED
sts_serial| 11| 100000| 100|0.09289715| PASSED
sts_serial| 11| 100000| 100|0.44233151| PASSED
sts_serial| 12| 100000| 100|0.74228831| PASSED
sts_serial| 12| 100000| 100|0.85785136| PASSED
sts_serial| 13| 100000| 100|0.16030108| PASSED
sts_serial| 13| 100000| 100|0.00323771| WEAK
sts_serial| 14| 100000| 100|0.58852039| PASSED
sts_serial| 14| 100000| 100|0.70323868| PASSED
sts_serial| 15| 100000| 100|0.03894230| PASSED
sts_serial| 15| 100000| 100|0.85451769| PASSED
sts_serial| 16| 100000| 100|0.29495284| PASSED
sts_serial| 16| 100000| 100|0.79662203| PASSED
rgb_bitdist| 1| 100000| 100|0.93478498| PASSED
rgb_bitdist| 2| 100000| 100|0.97950233| PASSED
rgb_bitdist| 3| 100000| 100|0.56044386| PASSED
rgb_bitdist| 4| 100000| 100|0.71018219| PASSED
rgb_bitdist| 5| 100000| 100|0.88729679| PASSED
rgb_bitdist| 6| 100000| 100|0.88606663| PASSED
rgb_bitdist| 7| 100000| 100|0.31777796| PASSED
rgb_bitdist| 8| 100000| 100|0.11847800| PASSED
rgb_bitdist| 9| 100000| 100|0.87424589| PASSED
rgb_bitdist| 10| 100000| 100|0.26387810| PASSED
rgb_bitdist| 11| 100000| 100|0.76563788| PASSED
rgb_bitdist| 12| 100000| 100|0.62314345| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.41188670| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.96139716| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.15209409| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.85756423| PASSED
rgb_permutations| 2| 100000| 100|0.43798937| PASSED
rgb_permutations| 3| 100000| 100|0.79582362| PASSED
rgb_permutations| 4| 100000| 100|0.84482179| PASSED
rgb_permutations| 5| 100000| 100|0.56754987| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.56893688| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.71710618| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.04322438| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.70410450| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.61294046| PASSED
rgb_lagged_sum| 5| 1000000| 100|0.00937777| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.01499892| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.41323462| PASSED
rgb_lagged_sum| 8| 1000000| 100|0.17986284| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.77422598| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.84668703| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.31899411| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.18327849| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.04663125| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.95238594| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.65816179| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.93352674| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.42125495| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.90269614| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.79005020| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.08941778| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.97545103| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.47051601| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.01421599| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.02382046| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.38335456| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.69167158| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.00906137| PASSED
rgb_lagged_sum| 28| 1000000| 100|0.22708952| PASSED
rgb_lagged_sum| 29| 1000000| 100|0.49280591| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.31680872| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.90355605| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.20762492| PASSED
rgb_kstest_test| 0| 10000| 1000|0.55959373| PASSED
dab_bytedistrib| 0| 51200000| 1|0.63968869| PASSED
dab_dct| 256| 50000| 1|0.50086423| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.91557618| PASSED
dab_filltree| 32| 15000000| 1|0.05590965| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.69303511| PASSED
dab_filltree2| 1| 5000000| 1|0.70893420| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.07691978| PASSED
The TRNG has no control commands, so it just output random numbers as long as the host ask for it. The USB communication is done via an FTDI chip, so your favorite OS is supported as long as an FTDI driver exist for it.
Supported OS according to FTDI’s website:
- Windows 8.1
- Windows 8.1 x64
- Windows 8
- Windows 8 x64
- Windows Server2012
- Windows Server 2008 R2
- Windows 7
- Windows 7 x64
- Windows Server 2008
- Windows Server 2008 x64
- Windows Vista
- Windows Vista x64
- Windows Server 2003
- Windows Server 2003 x64
- Windows XP
- Windows XP x64
- Windows ME
- Windows 98
- Linux
- Mac OS X
- Mac OS 9
- Mac OS 8
- Windows CE.NET (Version 4.2 and greater)
- Android
- Windows RT
FTDI D2XX driver download page: [http://www.ftdichip.com/Drivers/D2XX.htm](http://www.ftdichip.com/Drivers/D2XX.htm) (Note: the VCP driver is not needed).
Kidekin TRNG is tested on the following OS only:
- Windows 8.1 x64
- Windows 7 x64
- Debian x64 (running inside VirtualBox)
- Ubuntu 14LTS
This is a zip file bundling all documentation and software examples for Kidekin TRNG. The latest version and previous ones are available on kidekin’s website.
Click this link for direct download of latest version.
Most of the time Kidekin TRNG is recognized correctly by Windows which automatically download the right driver. The document trng_tips_windows present some tips if the automatic detection fails or you simply want to do the installation off-line.
The software presented in this section have been tested on Windows and Linux and should be able to run on any supported OS with minimal porting effort. They are located in the directory "application_notes_software\ftdi_d2xx". Each application note has a dedicated directory containing build script for windows (build.bat) and linux (build.sh). Those script creates a sub-directory to store intermediate object files and the executables, they therefore need write permission. The directory "common" contain things which are needed in several application notes.
Content of the "common" directory
- generic: this directory contain the C++ code of a thin wrapper around FTDI’s FTD2XX driver. It provides a straight forward interface to access Kidekin TRNG.
- linux: linux port of FTDI’s FTD2XX driver.
- windows: windows port of FTDI’s FTD2XX driver, including executable installer.
The program trng_capture allows to write random data to a file or the standard output. The standard output is a convenient way to directly feed random numbers to another software. That makes Kidekin TRNG accessible to virtually any programming language without resorting to write dedicated code in the target language. Binaries for windows and linux are provided as well as the C++ sources and simple build batch files and documentation (trng_capture.pdf). trng_capture allows to choose between binary or text output mode, in text mode the output is the conversion of random numbers to hexadecimal, so it looks like "A3BCFD67…" without any white space character.
This application note consist of two programs.
Programs:
- The program trng_server allows to send random data to another program running on another computer (or the same one).
- The program trng_client demonstrate how to connect to trng_server and writes random data to a file.
The client-server architecture is a way to easily access the TRNG with any programming language, all you need is to connect to a socket and request data. This is demonstrated with a java implementation of trng_client. Like in the capture application note, sources (C++ and java), binaries and documentation are provided (trng_server.pdf, trng_client.pdf). In addition, a step by step guide is provided to get both programs working together.
Linux provides convenient mechanisms to integrate hardware random generators, the application notes in this section show how to use them with Kidekin TRNG.
This application note show how to mound the TRNG as a Linux special device similar to /dev/random. After running an instal script, each time the TRNG is plugged-in, the device /dev/kidekin_trng will be mounted and ready for read operation in user mode. This is the most natural way to use the TRNG on linux: just read from the device as you would from /dev/random. Since the device has a specific name, it does not interfere with existing applications and your application can have exclusive use of it. The install script just copy a file containing udev rules, this works out of the box without installing any other software or packages.
This application note show how to feed Linux’s /dev/random with the TRNG. This way any program using /dev/random is seamlessly accelerated. This is especially useful on gaming servers or web servers which need to generate cryptographic keys. This is just some udev rules however it does require an additional package (rng-tools). An installer shell script is provided to copy the right files at the right places with minimal user effort.
First call to /dev/random is very fast because it just read buffered data, second call is way slower as the system is waiting to gather enough fresh entropy.
With Kidekin TRNG, first and subsequent calls to /dev/random are beyond 2MBits/s. In that experiment the last call read 10 mega bytes to minimize the effect of buffering on the performance measurement. Such request is possible only with Kidekin TRNG, without it /dev/random would take an unreasonable time. The performance achieved with /dev/random is slightly lower than reading directly /dev/kidekin_trng or using dedicated software however it allows to use standard software.
The definitions given here focus on the context of Kidekin TRNG, please refer to other sources to get an encyclopaedic definition.
- AES
Advanced Encryption Standard, as described in FIPS PUB 197
- CBC-MAC
Cipher Block Chaining Message Authentication Code. An algorithm originaly designed to authenticate data. In the context of Kidekin TRNG, it is used as post processing algorithm, as recommended in NIST’s SP800-90B.
- TRNG
True Random Number Generator, as opposed to Pseudo Random Number Generator (PRNG). A TRNG is a device whose output is unpredictable no matter how long one observe it. It is often desired that the output is also uniformly distributed, this is the case for Kidekin TRNG, with or without post processor.